那么这时候呢，我们觉得存一年时间有点儿久，我们想一个月一个月的存钱，这样取钱会变得方便，因为年利率为100%，换算到每个月后，利率就变成了1/12。我们依然存在这个银行中，那么一年后我们会拥有多少钱呢？因为我们按月存取，那么我们第一个月就会拥有100×(1+1/12)，那么第二个月就是100×(1+1/12)×(1+1/12)，那么在12个月后将拥有100×(1+1/12)^12，那么这个结果为多少呢，这个数值约为261元。
为什么同样是一个银行，同样的利率下数值差别这么大呢。这是因为我们在分月存取中，每个月我们的本金都在增加，我们利用新的本金用于计算时，将会使我们获得更多的钱。那么第一种情况叫做按年复利，而第二种情况叫做按月复利，二者是存在着较大的差别的。因此我们在选择年利率或者月利率计算时，结果会直接影响到选项。
那么我们做一个更加大胆的思考，按照这个存钱的思路，存取的次数越多，收益便越大。那么如果我们守在银行门口，只要它一开门就进去拼命地存钱取钱，一直到它下班为止，那么会不会收获无穷多的钱呢？如果不是无穷多的钱，那它又会是多少钱呢？
这个时候便是极限的思想了，记作存取次数为n，那么对应的利率便是1/n,这种情形下一年后将有100×(1+1/n)^n元。当时，数值将变成一个我们陌生又熟悉的数字100e，在以前的学习中，我们认识了e，但是并不知它从何而来，其实它就是来源于复利，当复利次数达到无穷时，我们发现数值开始趋近于一个特殊的数值，那么我们称这个数值为e，命名它为自然常数，因为它是客观存在的自然规律。并非由我们人为的创造，它本身具备数值。
那么涉及到e的问题以及上升到AP微积分的内容了，而在SAT2中，我们只是对按月复利和按年复利进行考察，比如下面一题：
这是一道正确率相当惨淡的题目，题目大意为我们有1000$存在年利率为8%的银行中，多少个月后我们将拥有2000$。这个题目同学们经常会有两种列法，设月数为x，第一种列法：
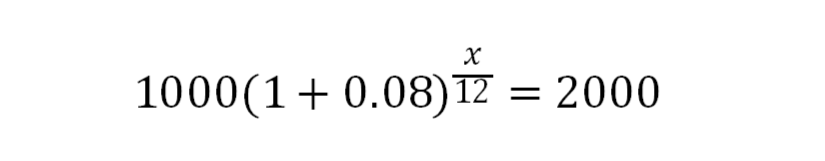第二种列法：
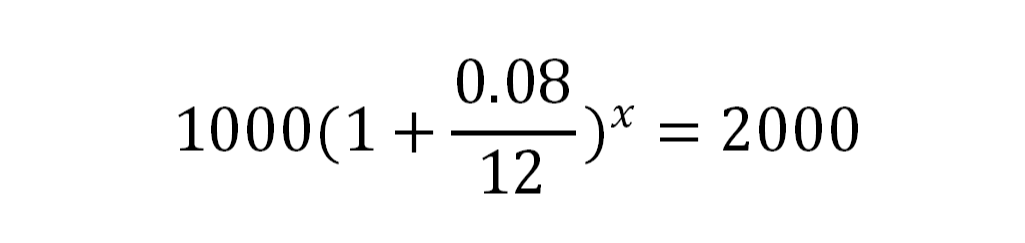第一种算法解出x=108，而第二种算法解出x=105，那么这两种方法哪个正确呢。注意到我们题干中有一个描述叫做，compounded monthly，这意味我们要按月复利，第一种列法的利率是年利率，而第二种列法的利率为月利率。因此正确答案为105。同时我们也可以清晰地知道，第二种方法之所以所需月份少，因为按月复利的本金变化速度快，可以用更少的时间达到我们的目标存款。
所以当我们勤快的存钱的时候，便可以收获更多的钱。但是非常不幸，银行也发现了这个问题，避免这种问题的发生，银行的月利率比年利率/12的数值要小。通过减小月利率的方式，来鼓励大家多存一段时间。所以具体银行利润要具体计算，不能一概而论。但学会这些这对于我们SAT2和AP考试，还是很有帮助滴~
TD福利
最后，TD君为大家送福利啦！为了让大家能够更加顺利地备考，我们为大家准备备考资料，免费送给大家！欢迎大家扫一扫下方二维码添加小马甲微信，回复「数学」免费获取，还能进入备考交流群与大家一起备考~已经添加TD客服马甲微信的同学直接领取即可
无需重复添加微信
